Now you may ask, how on earth do you get non-whole number dimensions? Well, that is the beauty of fractals, they don't conform to our usual concept of a dimension. To explore this let's take it from the basics.
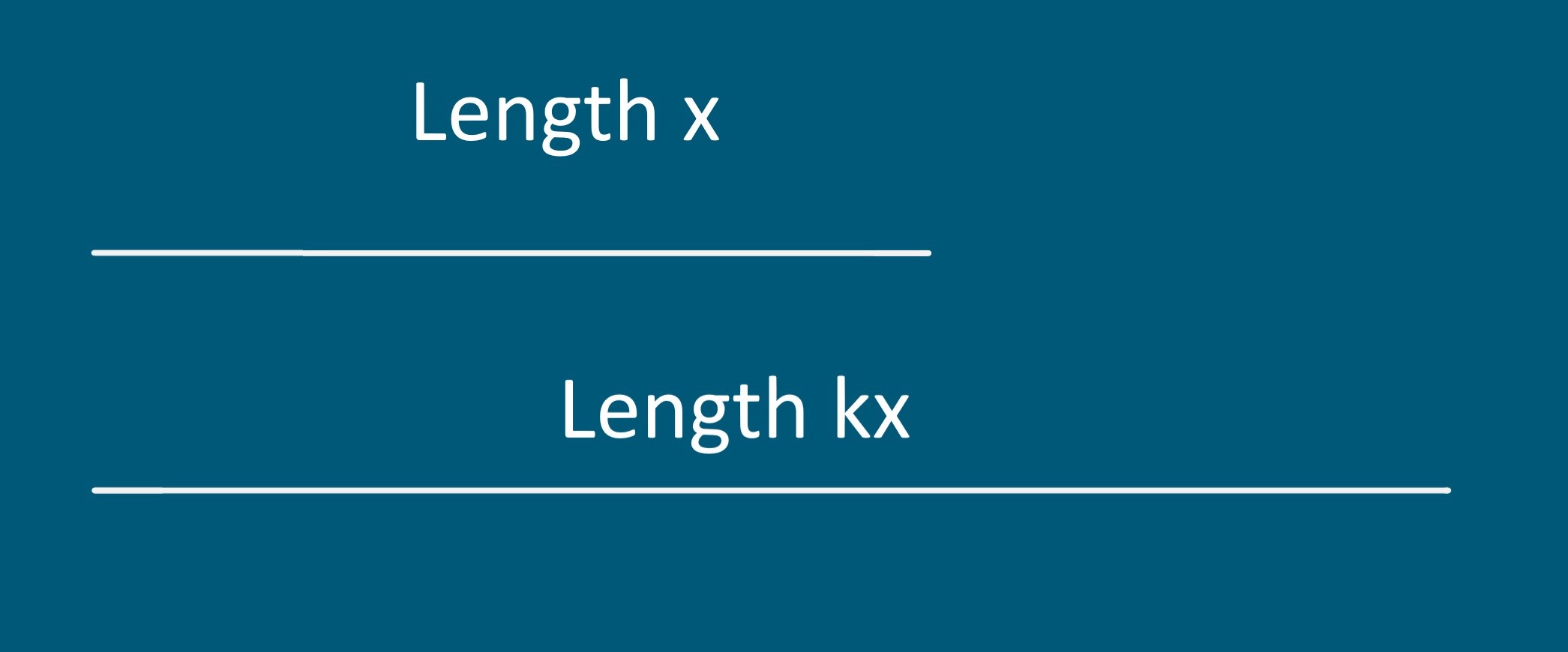
Here we can see the scale factor for a line is k. When you increase it's length but the scale factor for a square (two dimensional shape) is k².
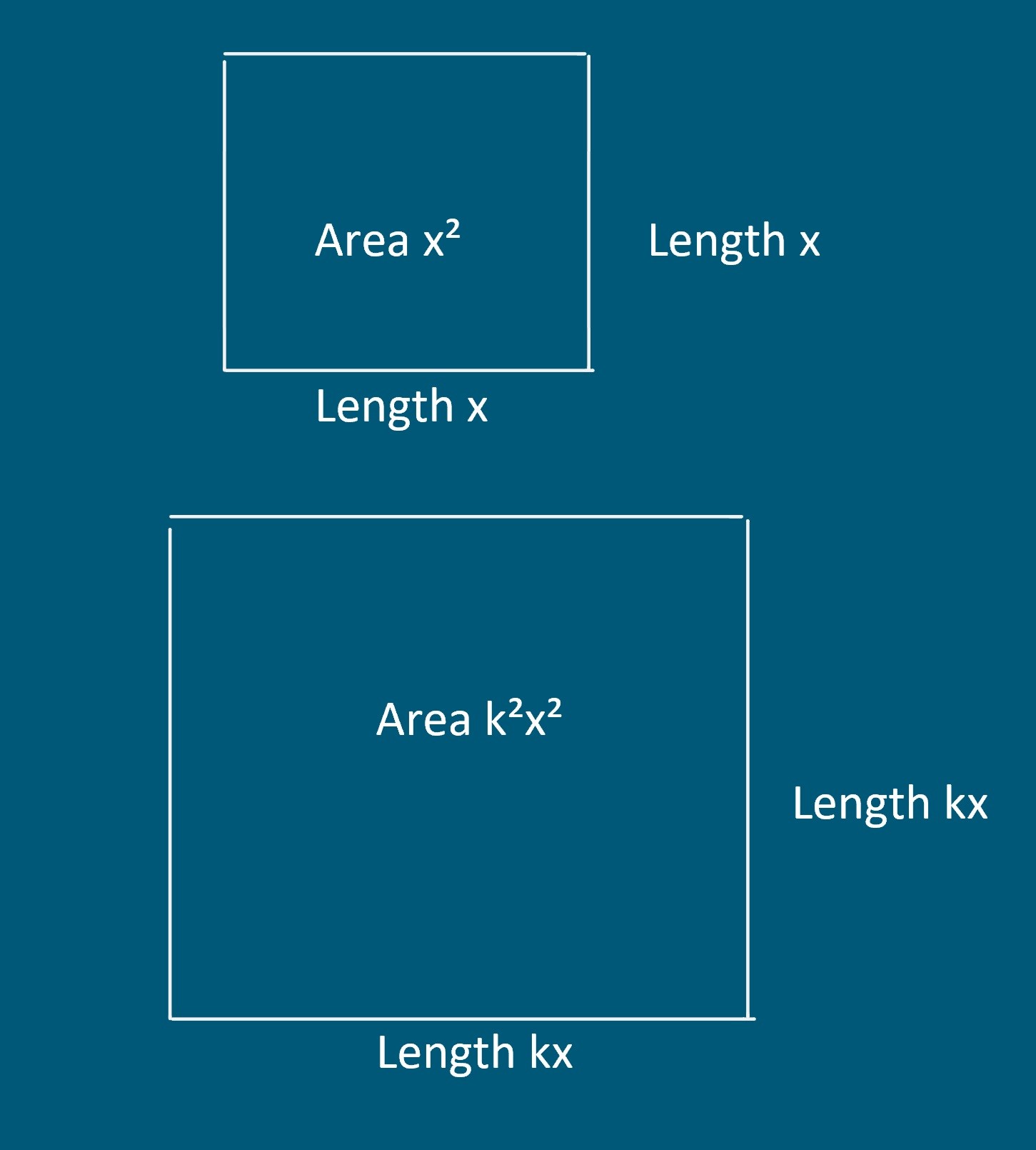
What is cool is that the scale factor of the line has a power of 1 (it's one dimensional) and the square has 2 (two dimensional). So why don't we apply this to a fractal.
If we take this Koch curve, we know that it will take some size x and if we scale it, it will become size xk^d where d is the number of dimensions. But if we look, the curve is made up of 4 smaller versions of itself, where each of these sections is 1/3 of the length of the curve.
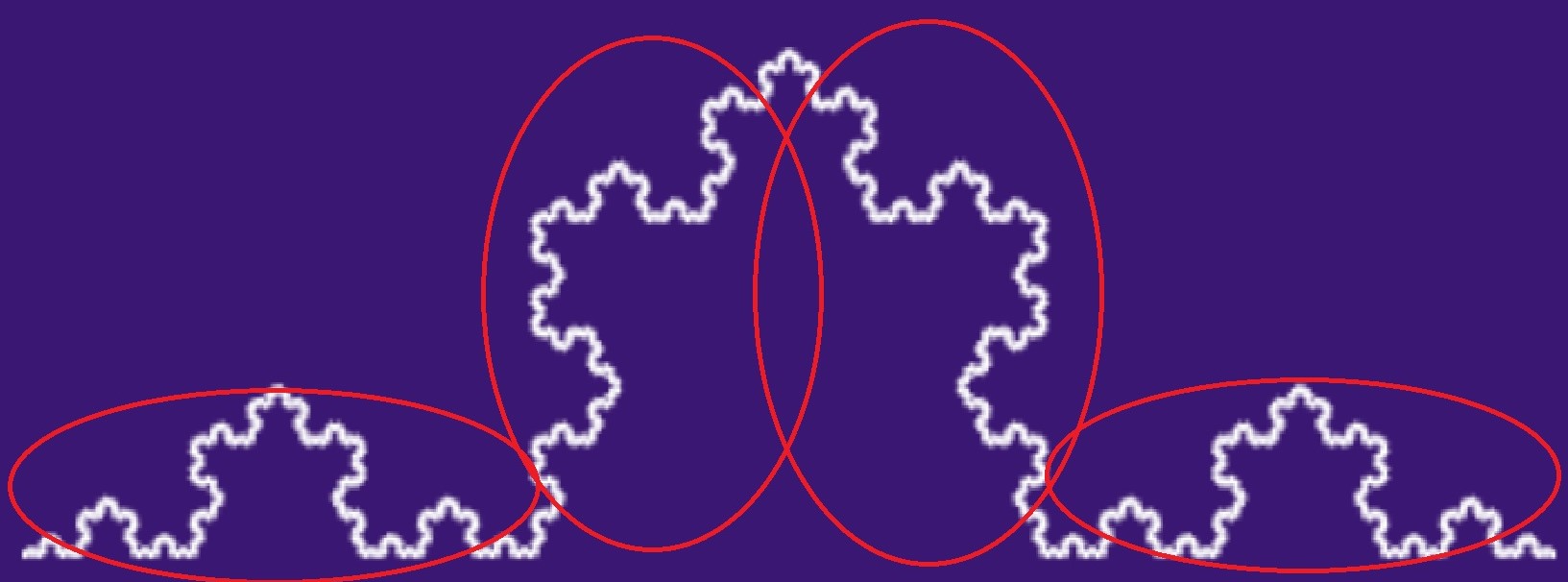

This means we have a shape made of k = 3 so (3^d)x is the area of the full curve. But it is made of 4 lots of x (where x is the area of the smaller section).
Putting this into mathematical terms (3^d)x = 4x
Here we can just cancel out the x meaning we have 4 = 3^d.
From here it's just a simple process, we take the log()
of both sides and re-arrange : d log(3) = log(4) => d = log(4)/log(3). This is approximately 1.262; meaning the curve has 1.262 dimensions.